Phán Đoán Phức - Phán Đoán - Logic Hình Thức (Logic Học Đại Cương)
Bài viết trước mình đã đi sâu vào vấn đề phán đoán đơn của chuyên đề PHÁN ĐOÁN PHỨC với những lí thuyết ngắn gọn, dễ hiểu và các ví dụ cụ thể. Ngày hôm nay, trong bài viết này, mình sẽ tiếp tục giúp các bạn hiểu nốt vấn đề còn lại của phán đoán là PHÁN ĐOÁN PHỨC
1. Khái niệm:
- Phán đoán phức là phán đoán được liên kết bằng các PHÁN ĐOÁN ĐƠN với nhau bởi những liên từ logic
- Chỉ có một liên từ logic thì đó là phán đoán cơ bản
- Có hai liên từ logic trở lên thì đó là phán đoán đa phức hợp
- Nhắc lại kiến thức bài hôm trước một chút:
Giá trị logic bao gồm:
+ Đúng = 1
+ Sai = 0
Giá trị logic chỉ có 2 đáp án hoặc đúng hoặc sai hoặc bằng = 0 hoặc =1. Ngoài ra không tồn tại giá trị khác.
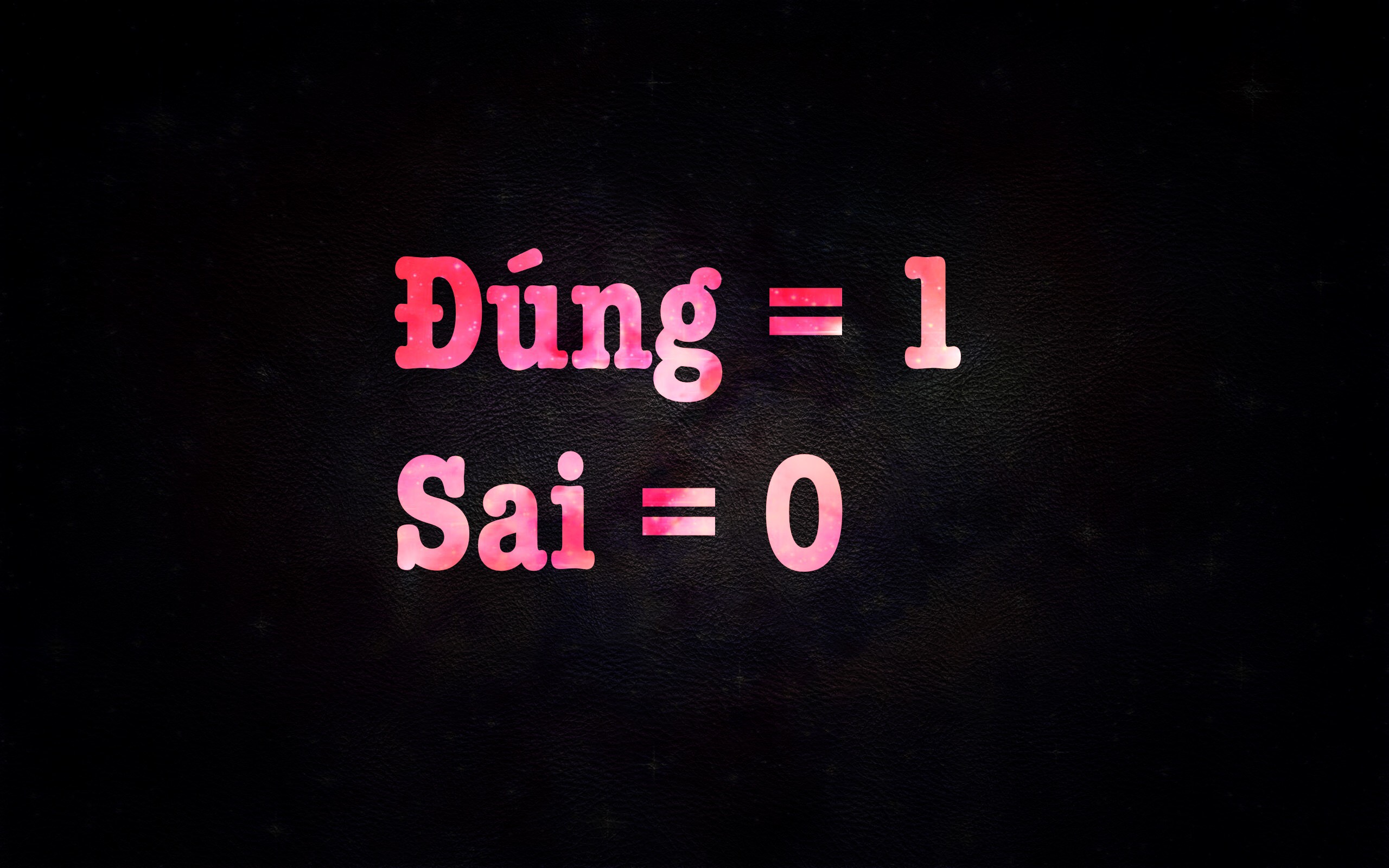
2. Phân loại:
2.1. Phép hội (a ∧ b) – đọc là a hội b
- Dấu hiệu nhận biết: trong phán đoán có xuất hiện các cụm từ: và, vừa…vừa, tuy…nhưng, chẳng những…mà còn, mà, song …
- Nguyên tắc: HỘI CHỈ ĐÚNG (=1) KHI CẢ HAI CÙNG ĐÚNG
Tức là:
+ Nếu a = 1, b = 1 (cả a và b =1 nghĩa là cả a và b cùng đúng vì đúng =1 sai mới = 0) thì a ∧ b (a hội b) sẽ bằng 1.
+ Nếu 1 trong hai giá trị a,b = 0 thì a ∧ b (a hội b) sẽ bằng 0 vì có chứa 1 giá trị sai là bằng 0
Ta có bảng giá trị logic như sau:
|
a |
b |
a ∧ b |
|
1 |
1 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
0 |
0 |
0 |
2.2. Phép tuyển (a ∨ b) – đọc là a tuyển b
- Dấu hiệu nhận biết: trong phán đoán có xuất hiện các cụm từ như là hoặc, hay là, ít nhất …
- Nguyên tắc: TUYỂN CHỈ SAI (=0) KHI CẢ HAI CÙNG SAI
Tức là:
+ Nếu a = 0, b = 0 thì a ∨ b = 0 (a,b là sai thì tuyển sẽ cùng sai)
+ Còn nếu một trong hai giá trị a,b có chứa 1 thì a ∨ b = 1
ü Ta có bảng giá trị logic như sau:
2.3. Phép kéo theo (a -> b) – đọc là a kéo theo bDấu hiệu nhận biết: trong phán đoán có xuất hiện cụm từ: nếu…thì
Nguyên tắc: KÉO THEO CHỈ SAI (=0) KHI 1 KÉO THEO 0
Tức là:
+ Nếu a = 1, b = 0 thì a -> b = 0 vì 1 kéo theo 0 là sai nên
bằng 0
+ Còn lại các trường hợp kéo theo ngoại trừ 1 -> 0 thì sẽ đúng
Ta có bảng giá trị logic như sau:
|
a |
b |
a ∨ b
|
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
|
a |
b |
a -> b |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
Dấu hiệu nhận biết: trong phán đoán có xuất hiện cụm từ: không
thể có chuyện
Ta có bảng giá trị logic như sau:
|
a |
ℸa |
|
1 |
0 |
|
0 |
1 |
Mẹo điền giá trị logic không cần nỗ lực nhiều:

3. Bài tập minh họa
Cho các công thức logic:
{[(a -> c) ![]() (b
-> c)] ∧ (a
(b
-> c)] ∧ (a ![]() b)}
-> c
b)}
-> c
a. Hãy tính giá trị logic của công thức với bộ giá trị a=1, b=0,
c=1
b. Hãy lập bảng đầy đủ giá trị logic của công thức
Giải:
a.
Thay các giá trị a=1,
b=0, c=1 vào công thức trên và thực hiện phép tính từ trái qua phải:
{[(a -> c) ∧ (b -> c)] ∧ (a ∨ b)} -> c
![]()
![]()
![]() {[(1 -> 1) ∧ (0 -> 1)] ∧ (1 ∨ 0)} -> 1
{[(1 -> 1) ∧ (0 -> 1)] ∧ (1 ∨ 0)} -> 1
![]() 1
∧ 1 ∧ 1
-> 1
1
∧ 1 ∧ 1
-> 1
![]() 1 ∧ 1
-> 1
1 ∧ 1
-> 1
1
![]() -> 1
-> 1
1
Vậy
với a=1, b=0, c=1 thì công thức trên có giá trị logic bằng 1
(những
dấu gạch trên là các bước tính chứ không viết vào bài nhé)
Quy ước:
![]()
![]()
![]()
![]()
![]()
![]() {[(a -> c) ∧ (b -> c)] ∧ (a ∨ b)} -> c
{[(a -> c) ∧ (b -> c)] ∧ (a ∨ b)} -> c
I II III
IV
V
VI
I: a -> c
II: b -> c
III: a ∨ b
IV: I ∧ II
V: IV ∧ III
VI: V -> c
Vì ở đây có 3 giá trị a,b,c nên ta lập bảng giá trị logic theo hệ nhị
phân (lũy thừa của 2). Ví dụ có 2 giá trị a,b thì xét 22 bằng
4. Có 3 giá trị thì xét 23, có 4 giá trị thì xét 24 … cứ
lũy thừa 2 lên tương ứng số giá trị.
Ở bài này có 3 giá trị
a,b,c thì xét 23 giá trị (tức là 8 giá trị)
Lập bảng giá trị logic: (Lập 4 giá trị a = 1 và lập 4 giá trị a = 0 vì có tất cả 8 giá trị)
(Giải thích cách làm:
I: a -> c
Để tính cột này thì thay
giá trị ở cột a kéo theo giá trị ở cột c
Lấy ví dụ: Dòng thứ nhất
(màu xanh) a=1, c=1 nên ta thay vào công thức I ta có đáp án I = 1 (xem công thức
ở trên)
Dòng thứ hai (màu đỏ) a=1, c=0 ta cũng thay vào công thức I = 0
vì phép kéo theo chỉ sai (bằng 0) khi 1 -> 0
II: b -> c
III: a ∨ b
IV: I ∧ II
Để tính giá trị ở cột này lấy giá trị vừa tính xong ở cột I tuyển
với giá trị cũng vừa tính xong ở cột II
Ví dụ a=1 ở cột I (màu vàng) tuyển với a=1 ở cột II (màu tím)
Là 1 ∧ 1 = 1
V: IV ∧ III
VI: V -> c
(tương tự)
(Mẹo: nếu kết quả cuối cùng bằng 1 thì công thức logic trên là đúng – phán đoán chân thực)

|
a |
b |
c |
I |
II |
III |
IV |
V |
VI |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
----------------------------
Hợp Tác Cùng YBOX.VN Truyền Thông Miễn Phí - Trả Phí Theo Yêu Cầu tại http://bit.ly/YBOX-Partnership
71,445 lượt xem
