“Lí Thuyết Trò Chơi” (Game Theory) là một nhánh của toán học ứng dụng. Theo đó ngành này nghiên cứu các tình huống chiến thuật mà đối thủ cố gắng vận dụng nhiều chiến lược khác nhau nhằm tối đa hóa kết quả nhận được.” (Wikipedia).

Hiểu một cách đơn giản, trong bất kì trường hợp nào con người ta cũng muốn đưa ra quyết định đem lại lợi ích cho mình nhiều nhất có thể. Đó là điểm mạnh đồng thời cũng là một hạn chế khiến cho chúng ta khó có thể đạt được kết quả cao trong “trò chơi” mang tên cuộc đời. “Lí thuyết trò chơi” ra đời để giải quyết vấn đề đó, nhưng vì ngành học này rất rộng nên nội dung bài viết này sẽ tập trung vào một nhánh nhỏ đồng thời cũng là nhân tố quan trọng nhất của “lí thuyết” này, chủ nghĩa duy lí.

Con người luôn suy nghĩ theo hướng Duy lí

Có hai tên trộm bàn kế hoạch đột nhập vào dinh thự của một người đàn ông giàu có trong vùng. Tuy nhiên chưa kịp thực hiện kế hoạch thì cả hai đã bị cảnh sát phát hiện và đem về tra hỏi. Vì hai nhân vật này vẫn chưa chính thức trộm một món đồ nào nên cảnh sát không có cách nào để buộc họ nhận tội. Bài toán được đặt ra lúc này là làm cách nào để ép hai tên trộm nhận tội nhằm trừ hại cho dân? Viên cảnh sát nghĩ ra một kế hoạch rồi đem hai tên trộm vào hai phòng xét xử khác nhau rồi đưa ra điều kiện với hai tên trộm (tạm gọi là A và B).

Thế lưỡng nan của người tù là một bài toán nổi tiếng về "Lí thuyết trò chơi"

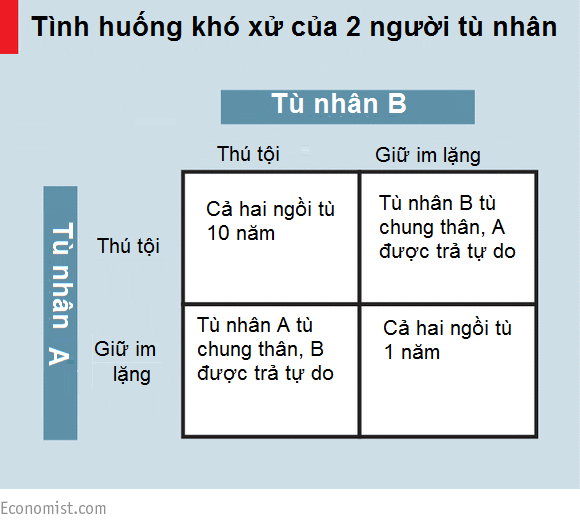
Nếu A và B cùng nhận tội, cả hai bị tuyên án 10 năm tù.

Nếu A tố cáo B, điều này đồng nghĩa với việc A bị oan còn B là chủ mưu, A được thả tự do còn B chịu án chung thân.

Nếu B tố cáo A, điều này đồng nghĩa với việc B bị oan còn A là chủ mưu, B được thả tự do còn A chịu án chung thân.

Nếu A và B cùng chối tội, cả hai bị tuyên án 1 năm tù giam.

Điều bất ngờ nhất là sau khi nhận được câu hỏi trên cả hai đều khai ra nhau dẫn đến kết quả đầu tiên, cả hai cùng chịu 10 năm tù giam vì đã tố cáo lẫn nhau. Bởi lẽ kết quả được thả tự do là một miếng mồi quá “hời” so với bất kì kết quả nào khác. Và chính nó là kẻ đã dẫn đến kết quả cả hai cùng chịu 10 năm tù giam vì đã tố cáo lẫn nhau.

Thực tế rằng còn một kết quả khác tốt hơn cho cả hai tên trộm chính là cả hai cùng chối tội thì mỗi người sẽ chỉ phải chịu 1 năm tù giam. Tuy nhiên trên thực tế “kết quả hoàn hảo” không bao giờ xảy ra. Bởi lẽ ngay cả khi cả hai được thống nhất quan điểm từ trước thì ngay khi một người im lặng người kia sẽ ngay lập tức tố cáo để dành sự tự do cho riêng mình. Bởi xét đến cùng thì tư duy của con người là duy lý, luôn muốn bản thân mình có nhiều lợi ích nhất có thể. Và lợi ích của người này bao giờ cũng là thiệt hại cho người khác, hiểu được điều đó quãng đường kế tiếp sẽ dễ đi hơn rất nhiều.

Rủi ro càng lớn, lợi nhuận càng cao

Như đã nói về chiến lược trong lí thuyết trò chơi, điểm hoàn hảo dành cho lợi ích của một người là không bao giờ xảy ra, bởi lợi ích của một người đồng nghĩa với thiệt hại về một người khác. Và điểm an toàn mà chúng ta hướng đến nhằm giảm thiệt hại cho mình nhiều nhất có thể lại chính là điểm nguy hiểm nhất khiến chúng ta không thể đi xa trong một cuộc đời đầy chiến lược.

"Crazy rich Asean" vận dụng rất nhiều lí thuyết trò chơi

Có một bộ phim vận dụng “lí thuyết trò chơi” mà tôi cực kì thích khi sử dụng lối tư duy này vào cuộc sống đời thường “Crazy rich Asean” (con nhà siêu giàu Châu Á). Theo đó nhân vật chính trong bộ phim là một giáo kinh tế chuyên về toán học ứng dụng. Cô quan niệm rằng “mọi người thường không chơi để thắng, họ chơi để không bị thua” và việc chúng ta cần làm là chơi tới cùng trong một ván đấu bất kể kết quả có ra sao. (Bạn có thể tìm hiểu về lí thuyết trò chơi rồi xem lại bộ phim thêm một lần nữa sẽ thấy rất nhiều góc nhìn rất khác so với truyền thông kể).

Bằng cách đó trong cuộc tỉ thí mạt chược với Eleanor mẹ chồng tương lai, mặc dù cô đã nắm trong tay quân “Bát sách” (tượng trưng cho Nick - người chồng) và có thể giành chiến thắng nhưng lại nhường nó cho mẹ chồng tương lai và nhận phần thua của mình. Bởi cô biết rằng:

Nếu mình giành được “bát sách” – anh ấy sẽ phải đối đầu với cả gia đình mình và sống không hạnh phúc cả quãng đời còn lại.

Nếu Eleanor giành được “bát sách” – Nick sẽ oán hận Eleanor suốt cả cuộc đời.

Có thể nói Rachel đã rất chiến lược khi cho Eleanor thấy trước kết quả của cuộc chiến để có được sự chấp thuận của cô. Đây là một ván bài rất hay, nó chứa đựng cả những triết lí trung hoa cũng như “lí thuyết trò chơi” của toán học ứng dụng trong cùng một ván đấu. Theo đó việc giành kết quả hoàn hảo ít rủi ro, tức giành Nick về tay mình chưa chắc đã tốt mà theo đó đôi khi chúng ta có thể cân nhắc những lựa chọn rủi ro nhưng lại đem về kết quả xứng đáng. Bởi trong “lí thuyết trò chơi”, rủi ro đi kèm với lợi nhuận, rủi ro càng lớn, lợi nhuận càng cao.

Tôi đã lấy lại thế cân bằng trong cuộc sống như thế nào?

Tôi lớn lên từ những quyển tạp chí, trưởng thành từ bộ phim huyền thoại “devil wear prada” với ước mơ sẽ trở thành một biên tập viên tạp chí. Đấy có thể là chuyện bình thường với người khác nhưng với một đứa con trai ở những làng quê nghèo phố núi, đấy là một điều lập dị. Những ước mơ đi xa so với gia cảnh và tài chính của gia đình là một điều viễn vông và nghiễm nhiên trở thành đề tài cho người khác phán xét. Bằng một cách nào đó, tôi của tuổi 17 nhiễm nhiên rơi vào bài toán “thế lưỡng nan của học sinh trung học” mà phải mất rất lâu tôi mới có thể tìm ra được câu trả lời.

Nếu chọn theo học nghề tại quê nhà, tôi sẽ giống người khác. Sẽ ra trường vào năm 22 tuổi, có một công việc “nhàn nhàn”, sẽ không bị phán xét. Sẽ giảm rủi ro mình nhận vào nhiều nhất có thể và quan trọng nhất, tôi sẽ không bị thua.

Nếu tôi chọn lựa theo đuổi con đường của riêng mình, tôi sẽ phải tự mày mò mọi thứ. Sẽ đối diện với nhiều vấn đề về kinh tế, rủi ro. Đây là con đường có thể đem lại nhiều lợi nhuận nhất nhưng cũng rủi ro nhất.

Và hiển nhiên theo tư duy duy lí, tôi của tuổi 17 đã lựa chọn con đường  nhằm giảm thiểu rủi ro nhiều nhất có thể, ở lại quê nhà. Đó là con đường an toàn, không rủi ro nhưng đồng thời cũng không mang về chút lợi nhuận nào. Tôi không hề biết mình là ai, muốn gì cũng như sẽ đi về đâu.

Mãi cho đến khi chấp nhận mất mát để đi khỏi điểm “an toàn” nhằm đẩy bản thân mình ra khỏi những trống rỗng. Tạm thời sẽ bỏ qua giai đoạn này một chút vì đây là giai đoạn “tích lũy kiến thức để tạo ra những bước nhảy cần thiết trong chiến lược trò chơi”. Bởi chỉ khi đủ kiến thức và tỉnh tảo để đối diện với những rắc rối có thể xảy đến khi bước khỏi vùng an toàn, con người ta mới đủ tư cách để nói mình sẽ trở thành ai và đi về hướng nào.

"Điểm nguy hiểm nhất là điểm tạo ra nhiều lợi nhuận nhất"

Một lời khuyên là khi còn trẻ, hãy tỉnh táo để nhìn giữa “điểm an toàn” và “điểm lợi nhuận”, khi chưa có đủ kiến thức và bản lĩnh tuyệt đối đừng vội vã ra khỏi điểm an toàn. Bởi đó là cách nhanh nhất để dẫn đến rủi ro tệ nhất khi không xem xét chiến lược và kết quả. Nếu có thể, hãy nới rộng điểm an toàn và tích lũy kiến thức. Hiểu rõ luật chơi để có một trò chơi hoàn hảo, chúng ta không chơi để hòa chúng ta chơi là để thắng.

Cuộc chơi của những người trẻ hiện đại

Có nhiều lí do để giữ con người ta ở lại điểm an toàn, thay vì những thử thách. Vì nó “an toàn” nhất, thiệt hại nhận về thấp nhất và quan trọng nhất không cần phải thay đổi qua nhiều. Nhưng xin nhắc lại thêm một lần nữa, điểm an toàn hoàn hảo không bao giờ xảy ra, bởi tư duy con người là duy lí. Cái lợi cho người này bao giờ cũng là thiệt hại cho người khác và điểm an toàn của người này bao giờ cũng sẽ bị xê dịch bởi người khác nhằm tranh giành lợi ích lẫn nhau. (Có thể hơi cực đoan một chút nhưng bạn có thể tìm hiểu thêm về toán học ứng dụng).

Có thể chọn thay đổi có thể không, có thể tham gia vào “thế lưỡng nan của học sinh trung học” bằng luật chơi của người khác hoặc can đảm đột phá tạo ra luật chơi của chính mình. Nhưng bao giờ cũng vậy, lợi nhuận tất đi kèm cùng rủi ro. Chuẩn bị chắc chắn cho một hành trình phía trước, can đảm đối diện và giải quyết hậu quả do chính mình tạo ra. Khi ấy chúng ta sẽ có một cuộc đời.

Và cuối cùng mặc dù lặp lại khá nhiều nhưng vẫn xin phép được nói thêm một lần nữa. Chúng ta tham gia trò chơi “cuộc sống” là để thắng vậy nên hãy đem về kết quả tốt nhất cho chính mình.

Tác Giả: Nguyễn Vũ Thiên Anh 

Kết bạn và theo dõi facebook của tác giả tại link: https://www.facebook.com/vuthienanh.98 

--------------------------------

Bạn đam mê viết lách, nhận giải thưởng (tổng trị giá 8 triệu VNĐ / tháng, sách, chứng nhận Social Impact Awards) và muốn được tạo thương hiệu cá nhân tới hàng triệu người trong cộng đồng của YBOX.VN? Xem chi tiết tại link: http://bit.ly/TrietHocTuoiTre-Info 

(*) Bản quyền bài viết thuộc về Cuộc thi Triết học Tuổi trẻ do Ybox đồng sáng lập và tổ chức. Khi chia sẻ, cần phải trích dẫn nguồn đầy đủ tên tác giả và nguồn là "Tên tác giả - Nguồn: Triết Học Tuổi Trẻ". Các bài viết trích nguồn không đầy đủ cú pháp đều không được chấp nhận và phải gỡ bỏ.